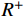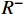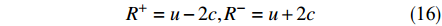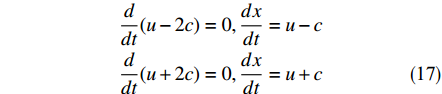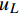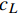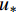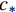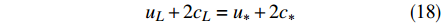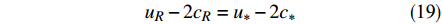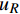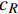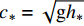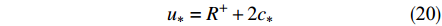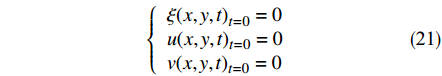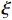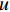2D numerical simulation of tidal current in the sea around Naozhou island based on shallow water equation
-
摘要:
以浅水方程为控制方程，对硇洲岛海域潮汐潮流进行了数值模拟。采用有限单元法离散求解浅水方程，将底坡源项归并到压力方程，保证了数值解具有和谐性；在限制水深法的基础上进行水深梯度修正，保证动量守恒，准确模拟了干湿变化过程；根据特征线理论建立边界潮位和潮流流速的关系，使得边界变量满足相容条件。研究结果表明：硇洲岛海域潮流为往复流，临近东海岛处海域流向呈NE-SW向，临近雷州湾处海域流向呈NW-SE向。
Abstract:The tidal current around Naozhou island is simulated with the shallow equation. The governing equations are discretized by a fractional finite element method using a characteristic-Galerkin procedure. In order to maintain the "well-balanced" property, the bottom slope source term was merged into the pressure equation. Moreover, a local bed slope modification technique is employed in drying-wetting interface treatments, the gradient of water depth was modified to ensure momentum conservation. Then the relationship between tidal level and velocity at the boundary was established based on the characteristic theory to ensure the accuracy of simulation. The results show that the tidal current around Naozhou island is the reciprocating-flow. The tidal current near the Donghai island flows along the NE-SW direction, while flows along the NW-SE direction near Leizhou bay.
-
Keywords:
- tidal current /
- shallow water equation /
- finite element method /
- harmoniousness /
- dry-wet boundary
-
硇洲岛面积约为56 km2，海岸线全长36 km，位于湛江市东南面，其东南面为南海，以西为雷州湾，北临湛江湾。前人对湛江湾海区开展了许多研究工作，陈达森等[1]研究了湛江湾海区流场特征及其对水环境的影响，指出湛江湾海区潮汐和潮流的主要性质；李拴虎[2]对湛江湾前海工程对湾口冲淤的影响做出了分析预测；李国杰等[3]对东海岛附近海域潮流场进行模拟，研究了工程建设对于工程区航道的影响，但目前对于硇洲岛潮流的研究还相对较少。
应用广泛的潮流数值模型包括Delft 3D[4]、ECOM[5]、ROMS[6]，FVCOM[7]和POM[8]等。考虑到硇洲岛海域垂直尺度远小于水平尺度，由三维数值模型经过垂向积分得到的二维数值模型具有更高的实用价值。因此，采用沿水深积分的浅水方程为控制方程，对硇洲岛海域潮流场进行模拟。本文采用FEM离散求解控制方程，为保证潮流计算的精确性，在求解时仍存在两个问题[9]：（1）数值解的和谐性；（2）边界的处理，包括干湿边界和开边界。
由于存在底坡源项，在求解浅水方程时可能会导致数值结果的不和谐，即在静水条件下，流速不为零，水位不一致。针对浅水方程的有限元数值解的和谐性，MAO等将底坡源项归并到压力方程[10]，保证了数值解具有和谐性。
干湿边界的处理是潮流预报的关键，如果处理不当，会导致计算发散。本文采用在限制水深法的基础上修正水深梯度的方式来模拟干湿变化过程。在潮流模拟中，开边界条件的处理会直接影响模拟精度[11]。缓流状态下出口边界的扰动会影响流场，需要保证边界变量满足相容条件，即沿特征线方向，特征不变量相等。本文根据特征线理论，建立了边界值和内点值的关系，推导了满足相容条件下的未知边界变量。
最后，对硇洲岛海域潮流进行了模拟，可为该海域水产养殖及海洋环境保护提供科学依据。
1 数值方法
1.1 控制方程
在平面二维模型中，水流为不可压缩牛顿流体，采用沿水深积分的浅水方程作为控制方程，考虑表面风切应力和科氏力，包括连续性方程与动量方程:
$$ \frac{{{\rm{\partial}} h}}{{{\rm{\partial}} {{t}}}}{\rm{ + }}\nabla \cdot {{U}}{\rm{ = 0}} $$ (1) $$ {\rm{\partial}} {{U}}{\rm{/}}{\rm{\partial}} {{t + }}\nabla \cdot \left( {{{u}} \otimes {{U}}} \right){\rm{ = }}\nabla \cdot {{\tau }}{\rm{ - }}\nabla \left( {{\rm{g}}{h^{\rm{2}}}{\rm{/2}}} \right){\rm{ + }}{{S}_{b}}{\rm{ + }}{S} $$ (2) 式中：h (m)为总水深；t (s)为时间；
$\nabla $ 为水平梯度算子；u (m/s)为水深平均的水平速度；U为守恒变量，U=uh，x、y方向分量分别为${{{U}}_x}$ 、${{{U}}_y}$ ；g (m/s2)为重力加速度，取9.81 m/s2; τ (N/m)为黏性项，$\tau = \mu (\nabla {{U}} + {\nabla ^T}{{U}})$ ；${{S}_{b}}$ (m2/s2)为底坡项；S (m2/s2)为源项，$S = {\tau _c} + {\tau _s}/\rho - {\tau _b}/\rho $ ；${\tau _c}$ (m2/s2)为科氏力项，x、y方向分量分别满足${\tau _{cx}} = {f_c}{{{U}}_y}$ ，${\tau _{cy}} = -{f_c}{{{U}}_x}$ ，${f_c}$ 为科氏力系数，${f_c} = 2\omega \sin \varphi $ ，ω (rad/s)为地球自转角速度，$\varphi $ 为当地纬度；${\tau _s}$ (Pa)为表面风应力，${\tau _s} = {C_w}\left| {{w}} \right|{{w}}$ ，w (m/s)为水面上10 m高处的风速；${\tau _b}$ (Pa)为底部摩擦项，${\tau _b} = - {\rm{g}}{n^2}|{{u}}|{{u}}/{h^{1/3}}$ 。1.2 离散格式
采用基于特征线法的离散格式[12]对方程(1)和方程(2)进行求解。引入波速
$c = \sqrt {{\rm{g}}h}$ 和两个与时间相关的变量${\theta _1}$ ，${\theta _2}$ ，将控制方程进行时间离散：$$ \frac{1}{{{c^2}}}\frac{{\Delta p}}{{\Delta t}} + \nabla \cdot {{{U}}^{（n + {\theta _1）}}} = 0 $$ (3) $$\frac{{\Delta {{u}}}}{{\Delta t}} + \nabla \cdot ({{u}} \otimes {{U}}) = \nabla \cdot {{\tau }} - \nabla {p^{（n + {\theta _2）}}} + {S_b} + S $$ (4) 式中：
$p = {\rm{g}}{h^2}/2$ ；${\theta _1}$ ,${\theta _2}$ 的取值范围均为$\left[ {0,1} \right]$ 。记
$F = {{u}} \otimes {{U}}$ ，$G = - {{{\tau }}^T}$ ，Q=−S，式(4)可改写为守恒形式：$$ \frac{{\partial {{U}}}}{{\partial t}} + \nabla \cdot {{F}} + \nabla \cdot {{G}} + Q = 0 $$ (5) 将式(5)沿特征线展开可得：
$$ \begin{split} \Delta {{U}} =\,& \frac{{\Delta {t^2}}}{2}{{u}} \cdot \nabla {(\nabla \cdot {{F}} + Q)^n} - \Delta t{(\nabla \cdot {{F}} + \nabla \cdot {{G}} + Q)^n}\\ &+ \frac{{\Delta {t^2}}}{2}{{u}} \cdot \nabla \left( {\nabla {p^{（n + \theta_2）}}} - {{{S}}_b} \right) - \Delta t\left( {\nabla {p^{（n + {\theta_2）}}} - {{{S}}_b}} \right) \end{split} $$ (6) 将增量
$\Delta {{U}}$ 分为如下两部分：$$ \Delta {{U}} = \Delta {{{U}}^*} + \Delta {{{U}}^{**}} $$ (7) $$ \begin{aligned} \Delta {{{U}}^*} =\,& \dfrac{{\Delta {t^2}}}{2}{{u}} \cdot \nabla {(\nabla \cdot {{F}} + Q)^n}\\ &- \Delta t{(\nabla \cdot {{F}} + \nabla \cdot {{G}} + Q)^n} \end{aligned} $$ (8) $$ \begin{split} \Delta {{{U}}^{**}} =\,& \frac{{\Delta {t^2}}}{2}{{u}} \cdot \nabla \left( {\nabla {p^{（n + {\theta _2）}}} - {{{S}}_b}} \right)\\ &{ - \Delta t\left( {\nabla {p^{（n + {\theta _2）}}} - {{{S}}_b}} \right)} \end{split} $$ (9) 中间守恒变量增量
${\Delta {{U}}}^*$ 由(8)求得，采用伽辽金加权余量法进行离散可得：$$ \begin{split} &\int {{{{N}}^T}} {{N}}d\Omega \Delta {{{{\bar U}}}^*} = - \Delta {{t}}\int {{{{N}}^T}} {{G}} \cdot {{n}}d\Gamma \\ &{ - \Delta {{t}}\left[ {\int {{{{N}}^T}} (\nabla \cdot {{F}} + Q)d\Omega - \int \nabla {{{N}}^T} \cdot {{G}}d\Omega } \right]}\\ &{ - \frac{{\Delta {t^2}}}{2}\int \nabla \cdot \left( {{{{N}}^T}{{u}}} \right)(\nabla \cdot {{F}} + Q)d\Omega } \end{split} $$ (10) 式中：
${{{{{\bar U}}}^*}}$ 表示变量在节点处的值；N为针对场U的权函数。值得注意的是，为保证数值解的和谐性，在中间守恒变量增量
$\Delta {{U}}^*$ 的计算中忽略了压力项和底坡项的影响，将压力梯度项和底坡项合并至压力方程中求解，即：$$ \Delta {{{U}}^{**}} = - \Delta t\left( {\nabla {p^{（n + {\theta _2）}}} - {{{S}}_b}} \right) $$ (11) 令
${{{U}}^{n + {\theta _{\rm{l}}}}} = {{{U}}^n} + {\theta _1}\Delta {{{U}}^*} + {\theta _{\rm{1}}}\Delta {{{U}}^{**}}$ ，并代入式(3)，可得：$$ \begin{split} &\frac{1}{{{c^2}}}\frac{{\Delta p}}{{\Delta t}} + \nabla \cdot \Bigr[ {{{{U}}^n} + {\theta _1}\Delta {{{U}}^*}} \\ &\left. { - {\theta_1}\Delta t\left( {\nabla {p^{（n + {\theta_2）}}} - {{{S}}_b}} \right)} \right] = 0 \end{split} $$ (12) 根据标准伽辽金方法进行空间离散，即：
$$ \begin{split} {{RHS}} =\,& \Delta {{\bar p}^n}\int {N_p^T} \frac{1}{{{c^2}}}{N_p}\frac{1}{{{c^2}}}{N_p}d\Omega \\ &+ \Delta {{\bar p}^n}{\theta _1}{\theta_2}\Delta {t^2}\int \nabla {N^T} \cdot \nabla Nd\Omega \end{split} $$ (13) 式中：
$N_p$ 为针对压力场的权函数；$\Delta {{\bar p}^n}$ 表示节点压力增量，右端项表达式满足：$$ \begin{split} {{RHS}} =\,& - \Delta t\int {{{N}}_p^T} \nabla \cdot \left( {{{{U}}^n} + {\theta_1}\Delta {{{U}}^*}} \right)d\Omega \\ &{ - {\theta_1}\Delta {t^2}\int \nabla {{N}}_p^T \cdot \left( {\nabla {p^n} - {{{S}}_b}} \right)d\Omega }\\ &{ + {\theta_1}\Delta {t^2}\int {{{N}}_p^T} \left( {\nabla {p^{（n + {\theta_2）}}} - {{{S}}_b}} \right) \cdot {{n}}d\Gamma } \end{split} $$ (14) 最后将式(9)进行空间离散，计算守恒变量增量的修正量
$ \Delta {{{U}}^{**}} $ ：$$ \begin{split} &\int {{{{N}}^T}} {{N}}d\Omega \Delta {U^{**}} = \\ &{ - \Delta t\int {{{{N}}^T}} \left[ {\nabla \left( {{p^n} + {\theta_2}\Delta {p^n}} \right) - {{{S}}_b}} \right]d\Omega } \end{split} $$ (15) 1.3 干湿边界
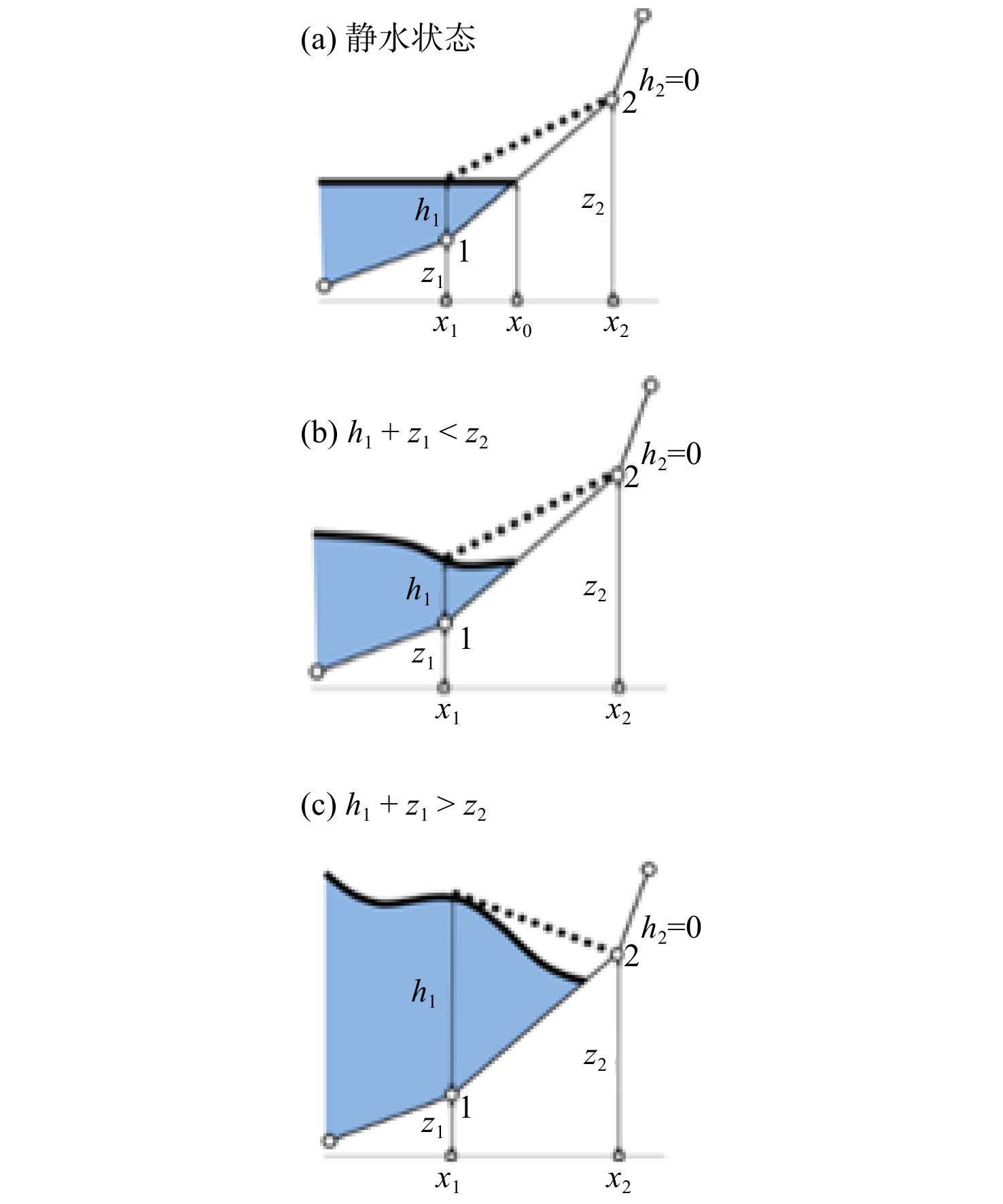
在有限元的求解过程中，由于采用固定的背景网格，根据限制水深法处理干湿边界时无法保证干湿边界恰好位于网格节点上，如图1所示。图中h为水深，z为底坡高程，虚线为数值求解的自由面，实线为实际自由面，二者间的差异会导致压力梯度计算错误，进而影响数值解的精度，甚至使得计算发散。为解决该问题，需按照干湿界面的具体情况进行水深梯度修正。当自由面如图1(a)和图1(b)所示时，将水深梯度修正为
$\nabla {h^*} = \dfrac{{0 - {h_1}}}{{{x_2} - {x_1}}} = \dfrac{{0 - {h_1}}}{{{x_0} - {x_1}}} = \nabla z$ 。当自由面如图1(c)所示时，按照下一时间步自由面的不同情况进行判断是否修正：若${h_1} + {z_1} \geqslant {z_2}$ 或${h_2}> 0$ 或${h_1} = {h_2} = 0$ ，不进行修正；若${h_1} + {z_1} < {z_2}$ ，在该时间步进行修正。1.4 基于特征线理论的潮位开边界
由于在潮流的实际观测中通常仅能给出潮位的精确信息，难以准确测定潮流流速，在给定边界条件时，仅有实测的潮位资料，缺少流速信息。在弗劳德数小于1，水流流态为缓流的情况下，边界的潮位信息必须要满足相容条件，否则会对上游流态产生影响。本节根据特征线理论推导出满足相容条件的边界流速取值。
对于平面二维边界，一般采用一维问题的近似处理。根据一维特征线理论，存在左右特征不变量
${R^ + }$ 和${R^ - }$ ，分别为：$$ {R^ + } = u - 2c,{R^ - } = u + 2c $$ (16) 并且存在如下关系：
$$ \begin{split} &\frac{d}{{dt}}(u - 2c) = 0,\frac{{dx}}{{dt}} = u - c\\ &\frac{d}{{dt}}(u + 2c) = 0,\frac{{dx}}{{dt}} = u + c \end{split} $$ (17) 对于边界而言，若左侧位于计算域内，根据右特征不变量沿特征线不变，则边界左侧内点的法向流速
$u_L$ 和波速$c_L$ 与边界上的法向流速$u_*$ 和波速$c_*$ 满足：$$ {u_L} + 2{c_L} = {u_*} + 2{c_*} $$ (18) 同理，若边界右侧位于计算域内，根据左特征不变量沿特征线不变，则：
$${u_R} - 2{c_R} = {u_*} - 2{c_*} $$ (19) 式中：
$u_R$ 和$c_R$ 分别为边界右侧内点的法向流速和波速。根据式(18)和(19)可以合理地处理开边界，使得边界变量相容。以边界右侧位于计算域内为例说明已知边界潮位情况下，确定边界流速：边界上给定水位h(t)=h*，可求得波速为$c_{*}=\sqrt{{\rm{g}} h_{*}}$ ，根据式(19)可知边界上法向流速为：$$ {u_*} = {R^ + } + 2{c_*} $$ (20) 2 潮流模拟
2.1 计算区域
本次模拟的区域为硇洲岛海域，除硇洲岛外，还包括东海岛、南三岛、雷州半岛及雷州湾、湛江湾、南海等在内的连续海域。海岸线和地形信息是影响潮流预测准确性的直接因素，因此高分辨的海岸线和水深信息是潮流模拟中必不可少的。本文采用从GSHHG (global self-consistent, hierarchical, high-resolution geography database)上获取的海岸线信息，分辨率为10 m，地形信息从GEBCO (the general bathymetric chart of the oceans)上获取，分辨率为15弧秒。根据已知的海岸线及地形信息，生成计算所需的有限元网格，如图2所示，为保证硇洲岛海域潮流预测的准确性，对硇洲岛附近的计算网格进行了加密。有限元模型共计103377个节点，102171个单元，局部加密共计30000个单元。
2.2 计算条件
根据相关文献[13]，海水运动粘滞系数取0.001 Pa·s，海床糙率取0.03125，湍流模型选择k-ε模型。
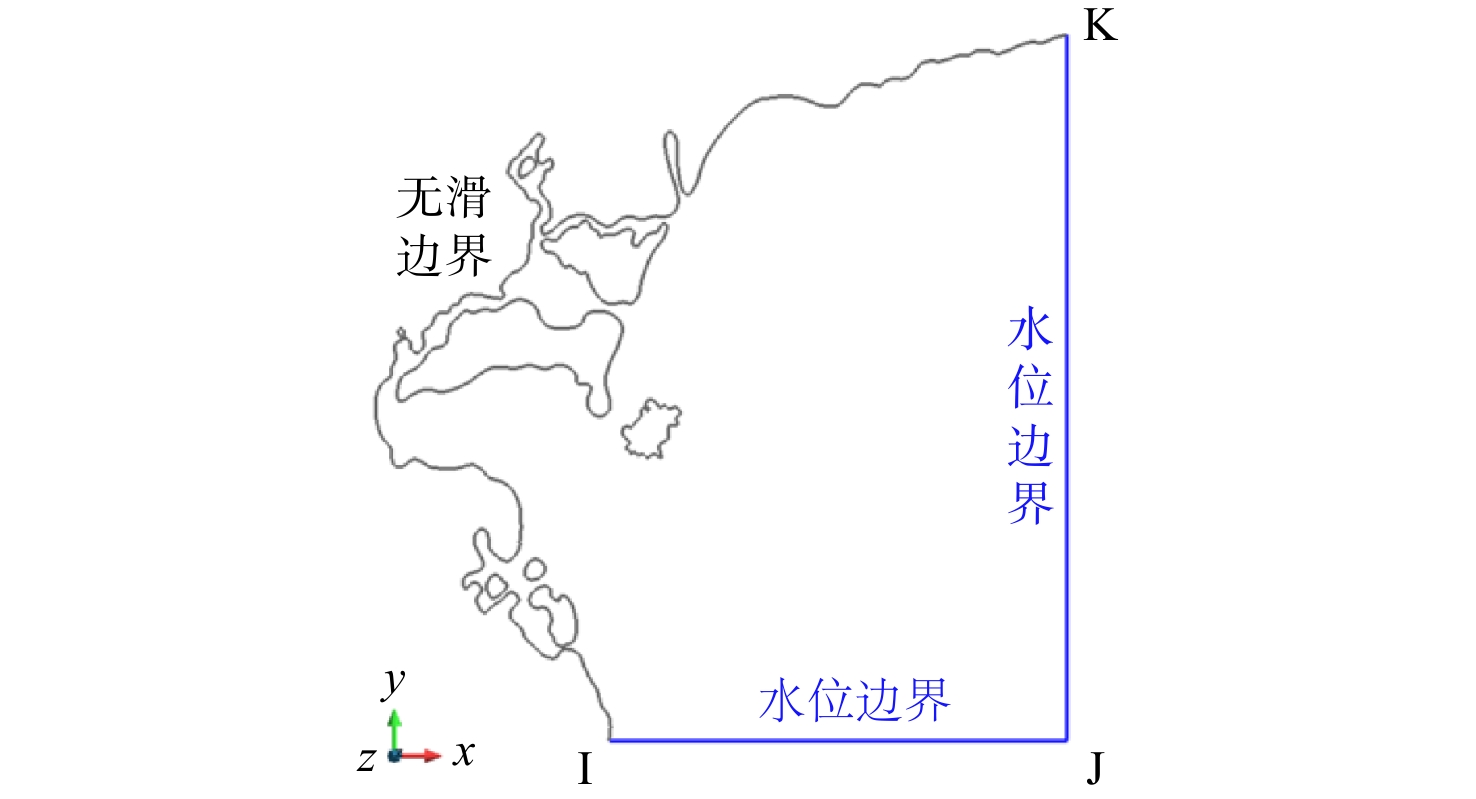
边界条件分为两部分，包括闭边界和开边界。闭边界即海陆分界线，取为无滑边界，开边界设定为水位边界，如图3所示。水位边界包括两条直线，需给定直线上每一点随时间变化的水位信息。图3中所示I、J、K三个点2019年6月9日8:00至6月11日0:00的实测水位信息由MIKE21自带卫星反演潮位数据提供，经过线性插值确定水位边界上每一点的水位信息。
潮流模拟自“冷态”启动，初始条件设置为：
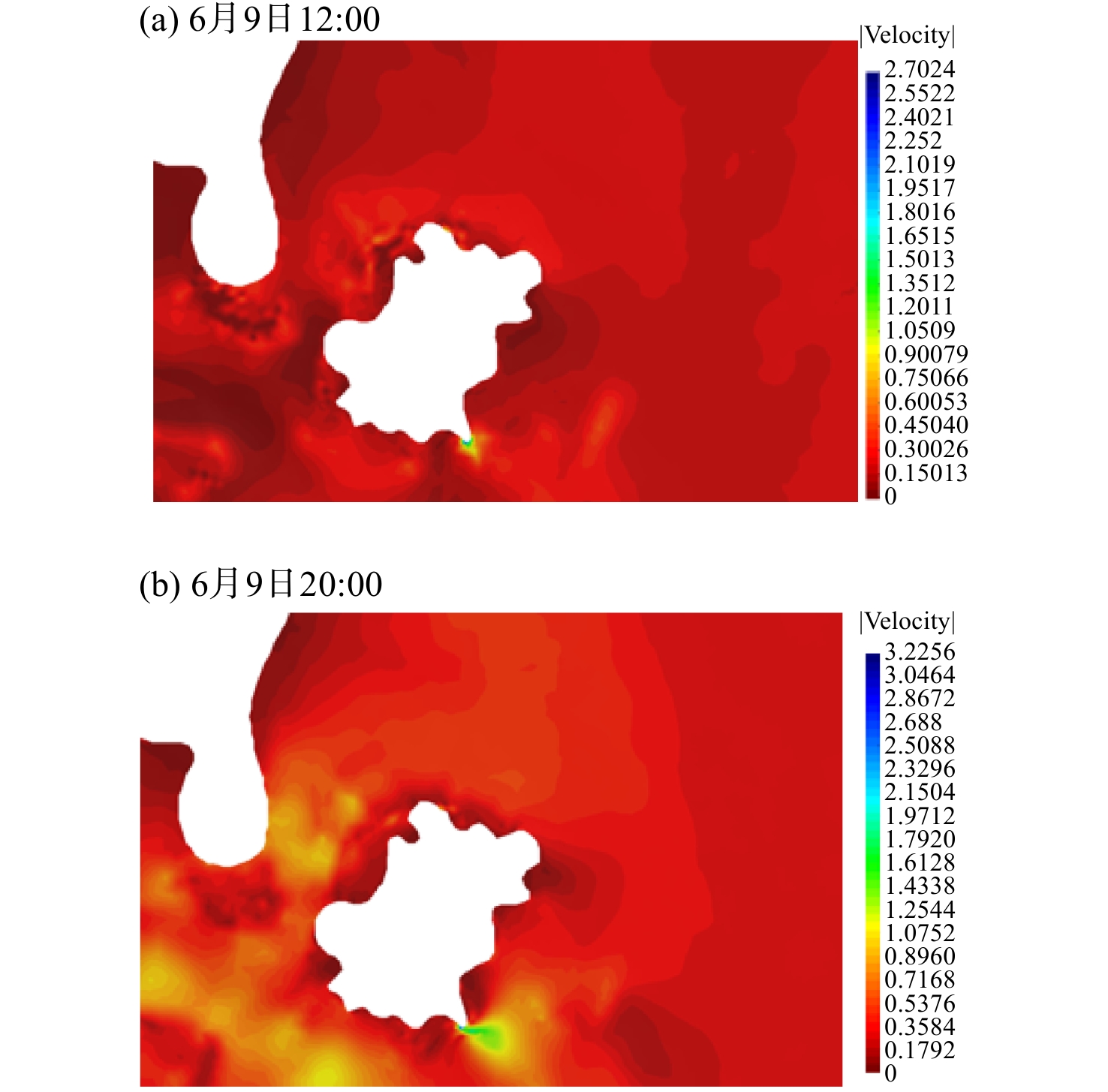
$$ \left\{ {\begin{array}{*{20}{l}} {\xi {{(x,y,t)}_{t = 0}} = 0}\\ {u{{(x,y,t)}_{t = 0}} = 0}\\ {v{{(x,y,t)}_{t = 0}} = 0} \end{array}} \right. $$ (21) 式中：
$\xi$ 为水位；$u$ 为x向速度；v为y向速度，不考虑温度、盐度等影响。2.3 模拟结果及特征分析
2.3.1 模拟结果
为进行模拟结果的对比验证，在硇洲岛附近选取了4个测点，如图4所示。
![]()
图 4 潮流模拟结果验证测点示意图Fig. 4 Schematic diagram of validation point positions for simulation results图5和图6分别对比了图4中所示的4个测点的模拟结果和由MIKE21反演模型提供的实测资料，包括潮位和流速大小，其中模拟结果包括根据特征线理论进行边界变量修正的模拟结果和未进行修正的模拟结果。4个测点潮位的改进后模拟结果与实测资料吻合较好，潮位峰值及相位基本一致，均为9日16:00左右达到第一次高潮，24:00达到第一次低潮，次日6:00达到第二次高潮，12:00达到第二次低潮，且高潮低潮潮位基本一致。图6所示的流速结果与实测资料存在偏差，主要原因是数值离散格式及精度的差别，但模拟结果与实测资料的误差在5%之内，模拟误差在可接受范围内。整体来说，本文的潮流模拟结果与实测资料吻合较好，模拟结果能够反映硇洲岛海域的潮流运动特征。而未改进的模拟结果与实测资料差别较大，说明边界变量需要满足相容条件，本文根据特征线理论推导的边界条件能够满足潮流模拟的需要。
2.3.2 潮流特征分析
（1）潮流运动形式
图7给出了4个典型时刻硇洲岛海域的流速矢量图，图7(a)时刻为涨潮流，海水由硇洲岛东部的南海涌入内海，使得水位升高，此时临近东海岛处海峡主流向呈NE向，硇洲岛南部海域主流向呈SE向。图7(b)时刻为落潮流，如图7(b)所示，海水由内海流经硇洲岛流向外海，使得水位降低，此时临近东海岛处海峡主流向呈SW向，硇洲岛南部海域主流向呈NW向，沿硇洲岛附近海峡进行往复流运动明显，而湾口附近则介于往复流和旋转流动之间。图7(c)和图7(d)与图7(a)和图7(b)类似，为潮位相对较低的高潮的涨潮落潮过程中的流速矢量分布。
![]()
图 7 硇洲岛海域典型时刻流速矢量图Fig. 7 Distributions of velocity vector in the sea around Naozhou island（2）潮流强度分布
为说明潮流强度分布，图8给出了第一次高潮涨潮和落潮时两个典型时刻的流速大小分布。如图8所示，涨潮时硇洲岛海域的流速值大致相等，在临近东海岛的海峡处由于水道狭窄致使流速相对偏高，最高为0.9 m/s。落潮时潮流强度的分布与涨潮时相差较大，除东海岛海峡外，硇洲岛南部与雷州湾相邻的海域流速相对偏大，最大流速约为1 m/s，其原因主要是海湾面积较小，潮汐受邻近海域潮波系统支配。
![]()
图 8 硇洲岛海域典型时刻流速大小分布云图Fig. 8 Distributions of velocity magnitude in the sea around Naozhou island3 结 论
（1）本文基于浅水方程，对硇洲岛海域潮流流场进行了模拟研究，模拟结果与实测资料吻合较好，说明本文所建立的潮流模型能够准确模拟具有复杂边界的潮流场。
（2）模拟结果表明：硇洲岛海域以往复流为主，临近东海岛处海域流向呈NE-SW向，临近雷州湾处海域流向呈NW-SE向。涨潮时流速分布大致相同，落潮时与东海岛相邻海峡及雷州湾方向海域流速值较大。
（3）硇洲岛海域潮汐以半日潮为主，潮差空间变化不大，分析原因主要是潮汐受邻近海域潮波系统支配，海湾面积较小。
（4）本文给出了边界变量满足相容条件的模拟结果，满足相容条件的模拟结果与实测值基本一致，而未改进的模拟结果则差别较大。
（5）本文验证了所用潮流模型在模拟硇洲岛海域潮流运动的精确性，为后续冲刷模拟以及海缆的受力分析提供水动力模型数据。
致谢：本文相关研究工作得到中国南方电网有限责任公司科技项目《海底电缆监测技术研究及应用—课题3：海底电缆水文环境监测、预测技术及应用系统开发》的资助，并得到河海大学水利水电学院赵兰浩教授和广东省电力设计研究院李健华博士的帮助，特此致谢。
-
![]()
图 4 潮流模拟结果验证测点示意图
Fig. 4. Schematic diagram of validation point positions for simulation results
![]()
图 7 硇洲岛海域典型时刻流速矢量图
Fig. 7. Distributions of velocity vector in the sea around Naozhou island
-
[1] 陈达森, 严金辉. 湛江湾海区流场特征及其对水环境的影响[J]. 科学技术与工程, 2006, 6(14): 2100-2103. doi: 10.3969/j.issn.1671-1815.2006.14.027 [2] 李拴虎. 湛江湾填海工程对湾口冲淤影响的分析研究[D]. 连云港: 国家海洋局第一海洋研究所, 2013. [3] 李国杰, 胡建平. 湛江东海岛近岸潮流场数值模拟[J]. 水道港口, 2007, 28(5): 325-330. doi: 10.3969/j.issn.1005-8443.2007.05.005 [4] LESSER G R, ROELVINK J A, VAN KESTER J A T M, et al. Development and validation of a three-dimensional morphological model[J]. Coastal Engineering, 2004, 51(8/9): 883-915.
[5] BLUMBERG A F. A primer for ECOM-si[R]. Technical Report of HydroQual, Mahwah, New Jersey: HydroQual, Inc., 1994: 66.
[6] SHCHEPETKIN A F, MCWILLIAMS J C. The Regional Oceanic Modeling System (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model[J]. Ocean Modelling, 2005, 9(4): 347-404. doi: 10.1016/j.ocemod.2004.08.002
[7] COWLES G W. Parallelization of the FVCOM coastal ocean model[J]. The International Journal of High Performance Computing Applications, 2008, 22(2): 177-193. doi: 10.1177/1094342007083804
[8] MELLOR G L. Users guide for a three-dimensional, primitive equation, numerical ocean model[R]. Princeton: Princeton University, 2004.
[9] 毛 佳, 赵兰浩, 郭博文. 干湿区域求解浅水方程的和谐有限元格式[C]//第十三届全国水动力学学术会议暨第二十六届全国水动力学研讨会论文集——C计算流体力学. 上海: 上海《水动力学研究与进展》杂志社, 2014. [10] MAO J, ZHAO L H, XIN B, et al. A novel well-balanced scheme for modeling of dam break flow in drying-wetting areas[J]. Computers & Fluids, 2016, 136: 324-330.
[11] 张大伟. 堤坝溃决水流数学模型及其应用研究[D]. 北京: 清华大学, 2008. [12] ZIENKIEWICZ O C, WU J. A general explicit or semi-explicit algorithm for compressible and incompressible flows[J]. International Journal for Numerical Methods in Engineering, 1992, 35(3): 457-479. doi: 10.1002/nme.1620350303
[13] 徐振华, 雷方辉, 娄安刚, 等. 北部湾潮汐潮流的数值模拟[J]. 海洋科学, 2010, 34(2): 10-14. -
期刊类型引用(1)
1. 李恩赐，王磊，庄茜，蒋学炼，李绍武. 基于断面和阻力等效的桩群调流效果研究. 海洋环境科学. 2023(06): 935-943 . 
本站查看
其他类型引用(3)
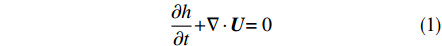
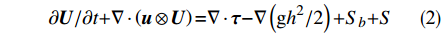
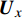
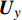
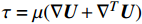
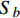
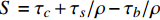
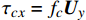
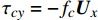
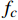
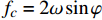
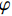
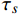
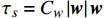
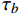
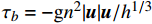
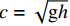
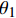
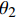
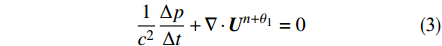
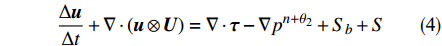
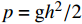
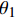
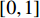
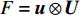
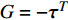
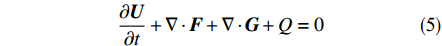
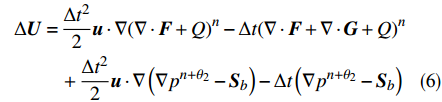
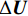
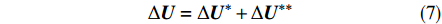
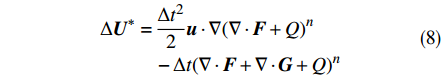
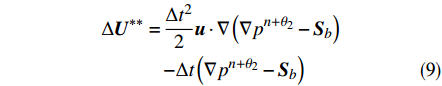
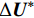
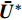
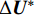
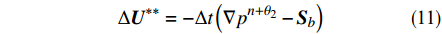
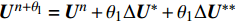
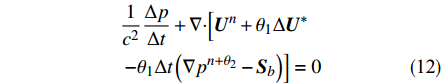
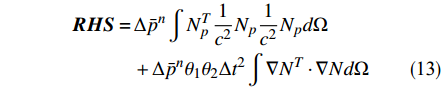
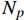
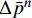
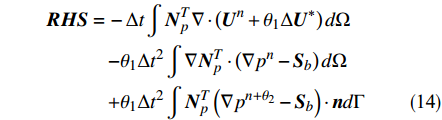
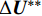
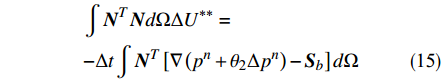
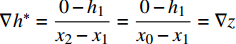
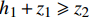
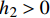
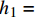
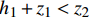
下载:
计量
- 文章访问数: 3063
- HTML全文浏览量: 2066
- PDF下载量: 42
- 被引次数: 4
